1 Key Concepts and their Modeling
We cannot speak about a model, a technology, not even about a modeling solution without a clear understanding of used concepts. Object, class, encapsulation, inheritance and polymorphism represent the basic concepts of the object model.
Object and class (to some extent) are independent (primary) concepts, encapsulation, inheritance and polymorphism are dependent concepts on the former, to the use and description of which they refer.
The infinite extension of the type system by the introduction of user defined types constitutes an essential feature of the object model. Therefore, type system management presents a crucial importance.
The terms instance and object are synonyms. Due to the fact the software systems objects and the relationships between them are created during execution, the system's architecture has a profound dynamic character. Persistent objects can be excepted from this rule.

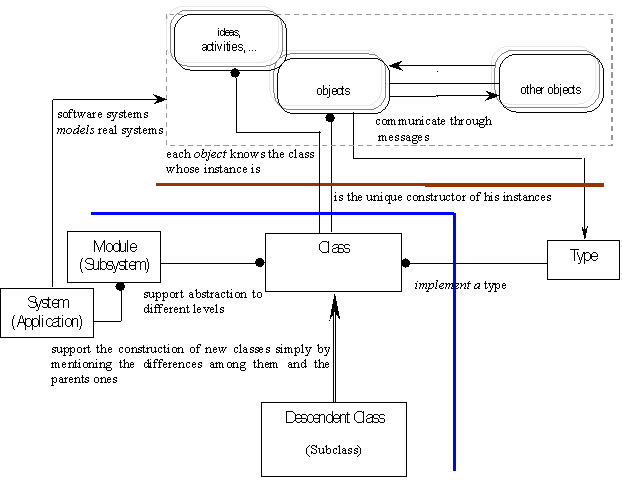
Figure 1.1 Software systems shape real systems
Object-oriented technology offers the best framework for modeling and implementing objects as application components. The feeling of naturalness given by the use of object-oriented technology (OOT) is one of the explanations for the attraction it exercises over a large number of people.
Definition 1.1.1
By object we understand something on which an action can be carried out or which can carry out an action. Objects are characterized by state, behavior and identity.
Internal objects should allow modeling of external objects and relationships among them as natural and simple as possible, in the conditions offered by software systems. From this point of view, inheritance is primarily important as a classification tool and only secondarily as an incremental description.
Object information should only be accessed or modified by the operation set defining object behavior. In fact, the only visible part of the object is made of operations and is called interface.
Definition 1.1.1.1
By encapsulation we mean the process of hiding the non essential features of an object. Naturally both the structure and the operation implementation are hidden.
Object Implementation Mode
Is very important as it has to support:
Definition 1.2.1
The class is a template allowing us to create new objects and to describe their features. (By features we understand both information referring to structure and behavior).
Due to the fact that objects of the same class have common definitions for operations, sometimes the class is called the object's type. However, type and class are two different notions.
Definition 1.2.2
By Abstract Data Type (ADT) we understand an object set defined by a set of operations. These are characterized by a signature and by the formal specification of the operation's "effect".
The last explanatory note is especially important because, as Meyer shows [Meyer97], it is not at all difficult to build an operation set with the same signature, but performing different things.
A class is a possible implementation of a type. This is why in type declarations, the class name designating the type implemented by this class is mentioned. A possible objection to this observation is that two classes with different structures can implement the same type. Because in the same modular unit two classes with the same name cannot be admitted, we can find ourselves in the situation when two classes with different names implement the same type. A class offers more information than the type it implements. We can look inside a class to see its internal structure. The interface concept introduced by Java, allows the identification of classes with different names, implementing the same type.
Definition 1.2.3
The class is an ADT implementation. It describes all the common features of its instances and allows the creation of new instances.
If we remember that one of OOP's basic objectives is reuse and that the structuring of classes in libraries is not made for only one application, we can conclude that a basic condition any class should fulfill is to support the unconstrained expression of all types of relationships that its instances have with instances of other classes in the system.
Unlike software objects, that represent an execution notion, classes represent a compilation notion. The main class purposes are:
In addition, a class should:
A consequence of the incremental class description is that the interface can be considered as being made up of two components: one inherited and the other one built in the class.
1.2.1 Behavior Incremental Specification
In the framework offered by object-oriented languages, new classes do not appear in a "deserted" world. Therefore, we should have a classification method able to express the relationships among classes. These relationships allow the description of the new components by simply mentioning the differences between them and the existing ones.
In traditional languages, reuse appears at the procedure level, while in OOL it is extended to class level and even to groups of classes. As a class contains both the operations and the data structure, class reuse is much stronger than procedure reuse.
Inheritance allows modifications to be made in a simple manner, as a property common to a group of classes is implemented into a single class. Modification of a common property requires its updating only in the common ancestor class.
Inheritance allows reuse of common features. Therefore it is promoted like a central reuse idea in the software industry. Although, inheritance is a very strong mechanism when used correctly, it is not a precondition for reuse. Inheritance proves extremely useful for easily carrying out the necessary system modifications. Another advantage of inheritance is the reduction of the system size by reducing informational redundancy. Models obtained this way are easier to understand. Adding a new class is easier done by describing the differences between them and the existing classes. However, the operation of adding new classes may imply inheritance hierarchy restructuring.
By extracting and sharing common features, classes can be generalized and placed higher in the inheritance hierarchy. When we want to add a new class, we have to find a parent class offering a part of the operations and the structure required for the new descendent class. We say that the descendent class specializes the parent.
In the process of class hierarchy building and restructuring, the root class and its close descendents, group the features of a great number of objects. These classes are built in such a way as to make up a features pool for descendents. They are called abstract classes because they cannot implement all the features. Formal specification of features properties allows avoiding this paradox: in the case when the root class does not have instance variables, the behavior can be altered by overwriting the methods, thus reaching the situation when, in fact, nothing is inherited. Actually, when conformity checking is missing, any method overwriting can lead to undesired situations. Unfortunately, the only language known to us that achieves formal specification is Eiffel. It is true that many languages offer mechanisms to forbid the modification of implementations in descendents. In the case of existing formal behavior specification, the class protocol will contain together with the methods' signature the formal specification associated to them.
Multiple inheritance is achieved when a class inherits from several classes. In the case of multiple inheritance, we must decide the way to solve possible conflicts, due to the name duplication of parent's features. The simplest solution is the identification of all the attributes name duplications and the interdiction of any kind of conflicts. In practice many other solutions have been adopted. In the case of multiple superclasses, there is more than one way for searching methods, and therefore the semantics of
super become more complicated.Because of this, the method searching may require the examination of a whole set of methods. In the case of multiple inheritance, these methods set form an oriented graph that sometimes can include cycles, reason for which a strategy for the examination of method graphs must be established.
Depending on the language type, some methods can be determined at the compilation time, (based on the information relative to types) others only at the execution.
Although the description and the implementation of the method search can be quite complex, it is conceived in such a way as to produce the illusion that methods are included directly in objects. When this illusion dissolves, confusions can appear relative to the language's semantics and implicitly to programming in the respective language.
1.3 Mathematical Modeling of the Subtyping Relationship
The correct understanding of the subtyping relationship, of its connection with the inheritance mechanism (subclass relationship) presents a particular importance. Several models have been built, each of them using different mathematical tools. In this thesis, two of the best known models are presented:
1.3.1 Ideals Subtyping Modeling
1.3.1.1 Dynamic binding and inclusion
Inheritance is a convenient mechanism that eliminates rewriting definitions that have already appeared in ancestors classes. But, the notion of inclusion associated to this mechanism, known as the subtyping polymorphism rule seems to be just as significant.
If
S is a subclass of C and s is an instance of S, then s can be considered as an instance of C.The rule, is based on the definition of polymorphism itself.
Definition 1.3.1.1.1
Polymorphism is a concept in the types theory, according to which a name (e.g. the declaration of a variable) can refer to objects from different classes bound by a "common superclass". Any object referred to by this name is able to answer differently to a common set of operations.
The rule stated above can also be written as:
If
S is a subclass of C and s: TS, then s: TC (1.3.1.1.1)TS <: TC
if and only if S is a subclass of C (1.3.1.1.2)This relation is intuitive if we consider it as the inclusion of a set of objects. For the time being, we presume that the relation satisfies the following property:
If
s: TS and TS <: TC, then s: TC (1.3.1.1.3)The property (1.3.1.1.3), called inclusion, is characteristic to subtype relations.
By inclusion, an instance of a type
TS can be seen as an instance of a supertype TC. We say that the value is included from the type TS to the type TC.The definition given in (1.3.1.1.2) to the subtype relation, that can be stated: "subclassing is subtyping", is a subclasses characteristic property in "classic" languages based on classes. As inheritance is related to subclassing, the definition (1.3.1.1.2) can also be read: "inheritance is subtyping".
Dynamic binding is found in all OOL, and therefore, can be regarded as one of the fundamental features of OOP. Dynamic binding is an important mechanism for object abstraction: each object itself knows how to behave.
An interesting consequence of dynamic binding is that inclusion doesn't have to make its effect over objects at execution.
1.3.1.2 Losing and finding type information
From a puritan point of view of the object-oriented methodology, dynamic binding is the only mechanism that allows obtaining advantages for the attributes that have been lost by inclusion. This position is often taken for abstraction reasons: no other knowledge must be obtained about objects except calling on their own methods. In the puritan approach, inclusion offers a simple and practical mechanism for hiding private attributes.
1.3.1.3 Covariance, countervariance and invariance
Let
AxB be the type of the pair whose left component has the type A, while the right component has the type B. The operations first(c) and last(c) extract the components from the left, and the right respectively, of an element c of type AXB.We say that "
x" is a covariant operator for both arguments.Property 1.3.1.3.1
If
A <: A' and B <: B', then AXB <: A'XB'
Proposition 1.3.1.3.1
If
A' <: A and B <: B' then, A ® B <: A' ® B'Proposition 1.3.1.3.2
If A = A' and B = B', then A*B <: A'*B'
1.3.2 A behavioral approach of subtyping - The model proposed by America
Weak typed OOL do not have an explicit notion for types and subtyping, while the existing strong typed languages identify subtyping with inheritance.
We are not interested in the way an object is internally represented, but in the ways in which it can be used. Consequently, we will define a type as a set of objects that have in common an intrinsic, externally noticeable property. By "intrinsic" we understand that the respective property does not change during an object's lifetime, and by "externally noticeable" that the property can be observed by sending the object a message. (Besides, this is the only way of interacting with objects in pure OOL).
Definition 1.3.2.1
We say that a type
s is a subtype of a type t if any object belonging to s will also belong to t. In other words, s is a subtype of t if any object that satisfies s 's specifications, will also satisfy t's specifications.
1.3.2.1 Specifying objects' behavior
Definition 1.3.2.1.1
Specifying a type
s is given by: S (the set of possible abstract states for objects of type s) and a set of methods specifications like {P}m(p1, ..., pn){Q}, where the precondition P = P(so, p1, ..., pn) describes the object's state before the method's application, and the postcondition Q = Q(s, so, p1, ..., pn, r) describes the object's state after the method's application. (s represents the current abstract state, so the abstract state before the mehtod's execution, p method parameters, r the sequence obtained after executing the get method).The meaning of this specification is that every object of type
s will have a method called m, so that, if the method is executed in a state in which the precondition P is true, then after the method's execution, the postcondition Q is true.An important problem is to see in what conditions objects of a class C are instances of a type
s, in which case we will say about the class C that it implements the type s.Definition 1.3.2.1.2
We say that the type
s is implemented by the class C, if the following conditions are fulfilled:Pof
replaces P. Each abstract state s is obtained after the application of the function f to a value of the concrete state C. The symbol "o" indicates "a sort of" functional composition of the function f: C ® S, with the precondition P, that applies the abstract states of the specification S in boolean values ("S ® {t, f}").
1.3.2.2 The subtyping relation
In the following, we will present the conditions in which a type
s is a subtype of a type t. In a first approximation, it is enough to require that for each method {P}m(This can be written as:
P ® P', Q' ® Q.In these circumstances, we can use any element of
s where an element of t is expected. When we send such an object a message "instancing" the method m, considering the object's type is t, the initial satisfaction of the precondition is guaranteed. From the implication P ® P' we can infer that the precondition P' is also true in s's specifications. After executing the method, the postcondition Q' from s will be satisfied, this implying Q 's satisfaction required by t.Generally, the type
t is specified using a mathematical domain T different from the mathematical domain S used in s's definition.Property 1.3.2.2.1
If a class
C implements a type s and s is a subtype of t, then C also implements t.
1.3.3 Changing arguments' type in method redefinitions
The combination between static typing and dynamic binding gives birth to delicate problems whose solving is not always ordinary. Two techniques can cause trouble: changing the arguments' type in redefinitions and hiding the descendent - a class' ability of restraining the export status for some features. In the thesis is presented the Meyer example [Meyer97] which demonstrates that the contravariate specialization of arguments' type can lead to obtaining software systems unusable in practice.
1.4 Conclusions
The main strength of the object model consists of creating the ideal framework for modeling. The correct understanding of the relationship between real (external) objects and software (internal) ones is extremely important.
The difficulty of abstract data types' rigorous and complete specification and lack of overwriting control are two main reasons negatively influencing reusability. Modeling elegance is another key factor. Unfortunately it is not sufficient. As it is known, any modeling makes simplifying suppositions. This is the reason for which part of the results offered by mathematical models cannot be used.
Models must be well known to understand their limitations and apply them whenever possible. Becoming aware of unsolved aspects incites to searching new solutions.